In the following sequences, figures are frequently presented
in pairs. The left figure in each pair is the front view-Escher's drawing's direction, whereas the right figure gives
a general view. Whenever a real, tangible model has been created, it will
be presented as a second pair to the right of the pair of computer rendered
images. The objects were physically realized with the aid of layered
manufacturing systems: a Z402 3D Printer from Zcorporation and a Stratasys FDM3000 printing machine.
Click on any image below to get the full size version of these images. In
addition, some models are also accompanied by AVI movies that present them from
a multitude of directions. Many of these movies are using the DivX CODEC which you can get free of charge
for private use from http://www.divx.com/divx/download.



 We start with the Penrose triangle object (also
independently invented by Oscar Reutersvard). There are several ways to build a
real geometry that will look like the Penrose triangle from a certain viewing
direction. This specific shape is reconstructed as a C^0 continuous sweep
surface with a square cross section that rotates as we move along the edges. As
will be shown below, the Penrose triangle plays a majosr role in M.C. Escher's
drawings. An STL geometry file, for those of you with layered manufacturing
devices, of this model, is available here
.
We start with the Penrose triangle object (also
independently invented by Oscar Reutersvard). There are several ways to build a
real geometry that will look like the Penrose triangle from a certain viewing
direction. This specific shape is reconstructed as a C^0 continuous sweep
surface with a square cross section that rotates as we move along the edges. As
will be shown below, the Penrose triangle plays a majosr role in M.C. Escher's
drawings. An STL geometry file, for those of you with layered manufacturing
devices, of this model, is available here
. 


 The impossible shape conveyed by the Penrose triangle
is the most well-known one. However, one can, with similar ease and with the aid
of a geometric modeling system, construct more complex natural extensions to the
Penrose triangle. Herein a Penrose rectangle is presented.
The impossible shape conveyed by the Penrose triangle
is the most well-known one. However, one can, with similar ease and with the aid
of a geometric modeling system, construct more complex natural extensions to the
Penrose triangle. Herein a Penrose rectangle is presented.


 Similarly and following the construction of a Penrose
triangle and Penrose rectangle, one can easily create an arbitrary Penrose
n-gon. Here, we will stop at a Penrose pentagon.
Similarly and following the construction of a Penrose
triangle and Penrose rectangle, one can easily create an arbitrary Penrose
n-gon. Here, we will stop at a Penrose pentagon. 


 Here we present another way to simulate and
realize geometry that looks like the Penrose triangle from a certain view. Here
is an avi
movie that shows this model rotated. An STL geometry file, for those of you
with layered manufacturing devices, of this model, is available here
.
Here we present another way to simulate and
realize geometry that looks like the Penrose triangle from a certain view. Here
is an avi
movie that shows this model rotated. An STL geometry file, for those of you
with layered manufacturing devices, of this model, is available here
. 


 Here is our realizable variant of Escher's Cube. If
you will look carefully enough, you will find this cube in Escher's original
Belvedere drawing. Here is an avi
movie that shows this model rotated.
Here is our realizable variant of Escher's Cube. If
you will look carefully enough, you will find this cube in Escher's original
Belvedere drawing. Here is an avi
movie that shows this model rotated. 


 Here is a variant of the Moebius Ring formed out of Escher's
duck tiling.
Here is a variant of the Moebius Ring formed out of Escher's
duck tiling. 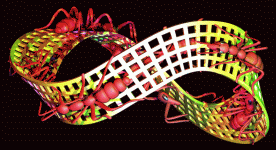

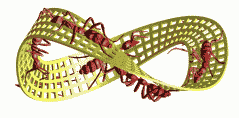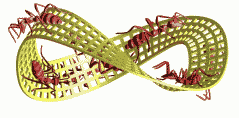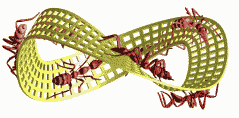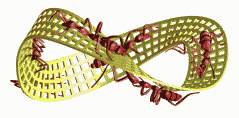





 Here is our physical realization of Escher's Waterfall. You can
also watch this object rotating in space in this avi
movie. This realization stems from using three joint Penrose triangles along
the water stream. Note also the way the house is warped so as to look natural
from this viewing direction (only).
Here is our physical realization of Escher's Waterfall. You can
also watch this object rotating in space in this avi
movie. This realization stems from using three joint Penrose triangles along
the water stream. Note also the way the house is warped so as to look natural
from this viewing direction (only).

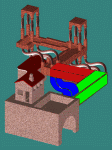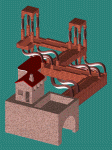
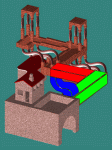 To better understand this, examine the pictures on the left. The
rightmost image shows the Penrose triangle only, from above; the leftmost image
shows the original Waterfall scene; and the middle image is a blend of the two.
In fact, the original Waterfall model presents three different and
connected such triangles. Also interesting in this image is the
house. When we examine the original Waterfall drawing, we see that the
house ends up behind the middle corner of the water path. In order
to accomplish this in our constructed image, the house's geometry is warped so
as to look straight only from the proper viewing direction. The house, as
well as the S shaped rods that look vertical from the original viewing
direction, were modeled as generalized sweeps by the geometric modeler.
To better understand this, examine the pictures on the left. The
rightmost image shows the Penrose triangle only, from above; the leftmost image
shows the original Waterfall scene; and the middle image is a blend of the two.
In fact, the original Waterfall model presents three different and
connected such triangles. Also interesting in this image is the
house. When we examine the original Waterfall drawing, we see that the
house ends up behind the middle corner of the water path. In order
to accomplish this in our constructed image, the house's geometry is warped so
as to look straight only from the proper viewing direction. The house, as
well as the S shaped rods that look vertical from the original viewing
direction, were modeled as generalized sweeps by the geometric modeler.


 Here is our physical realization of Escher's Belvedere drawing.
Again, this model looks like the original Escher drawing from one direction
only, whereas the (not so) vertical poles stretch from the far top to the near
bottom sides and vice-versa. This trick is somewhat similar to the trick we used
in the Penrose triangle but is somewhat simpler. You can also watch this object
rotating in space in this avi
movie.
Here is our physical realization of Escher's Belvedere drawing.
Again, this model looks like the original Escher drawing from one direction
only, whereas the (not so) vertical poles stretch from the far top to the near
bottom sides and vice-versa. This trick is somewhat similar to the trick we used
in the Penrose triangle but is somewhat simpler. You can also watch this object
rotating in space in this avi
movie. 

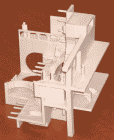
 Here is our physical realization of Escher's Relativity drawing
that was modeled with the aid of Oded Fuhrmann, Technion. This model is
different compared to many of the above in the sense that it is a regular model
(with stair cases all over the place :-). We need no special view direction, for
this model to look like the original Escher drawing.
Here is our physical realization of Escher's Relativity drawing
that was modeled with the aid of Oded Fuhrmann, Technion. This model is
different compared to many of the above in the sense that it is a regular model
(with stair cases all over the place :-). We need no special view direction, for
this model to look like the original Escher drawing.